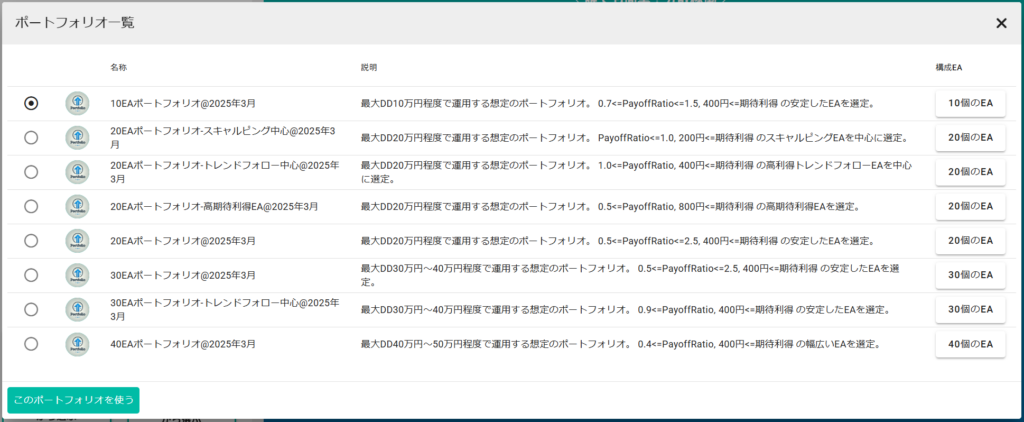
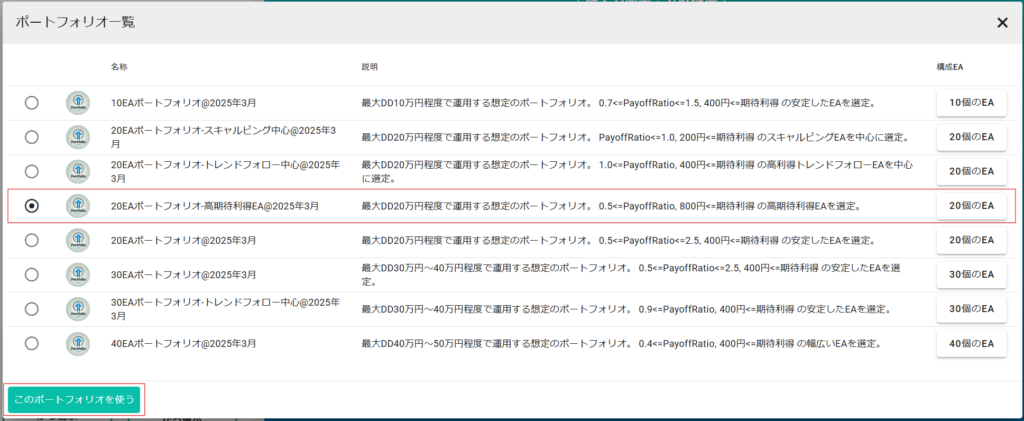
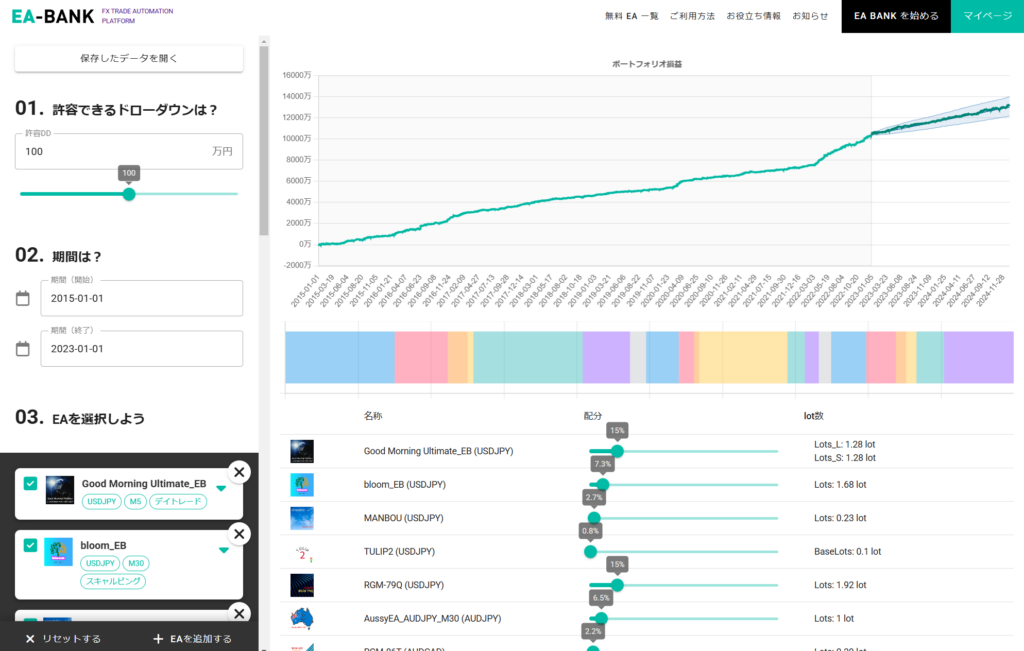
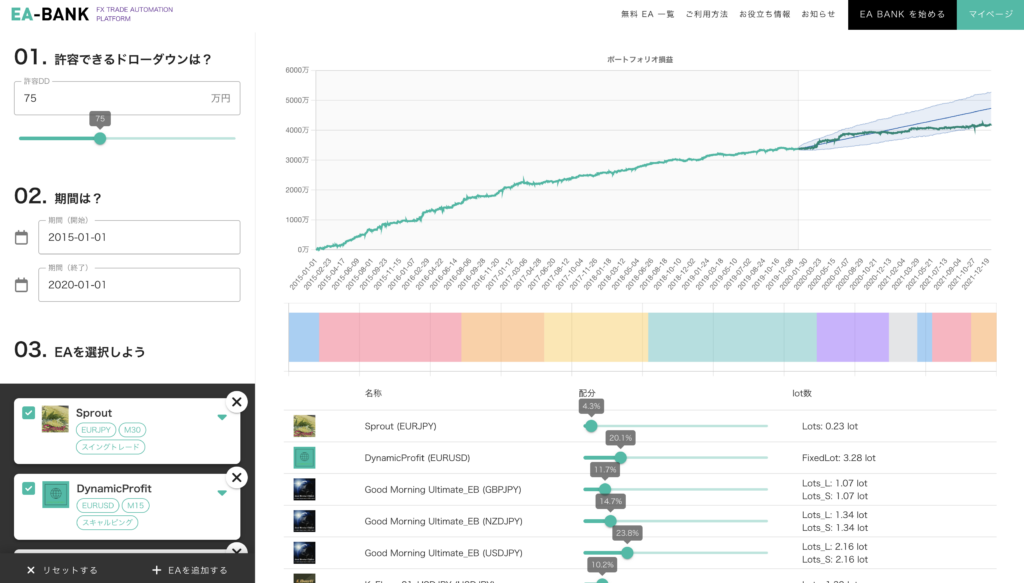
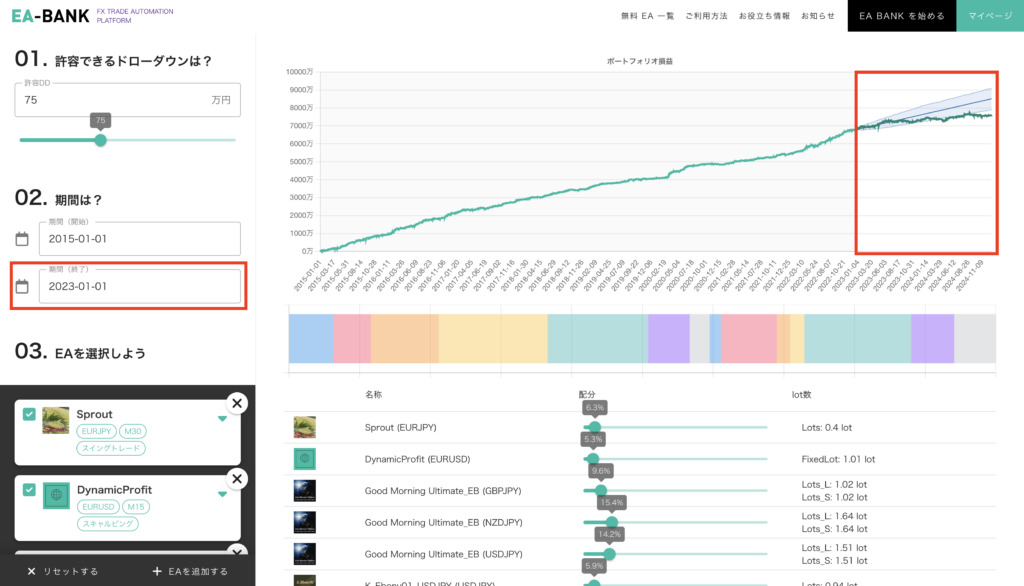
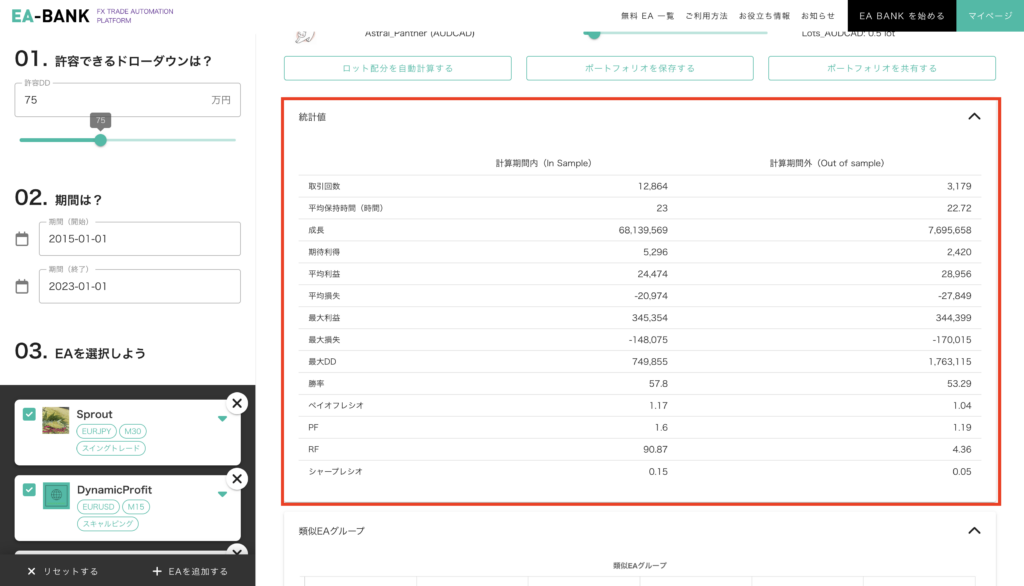
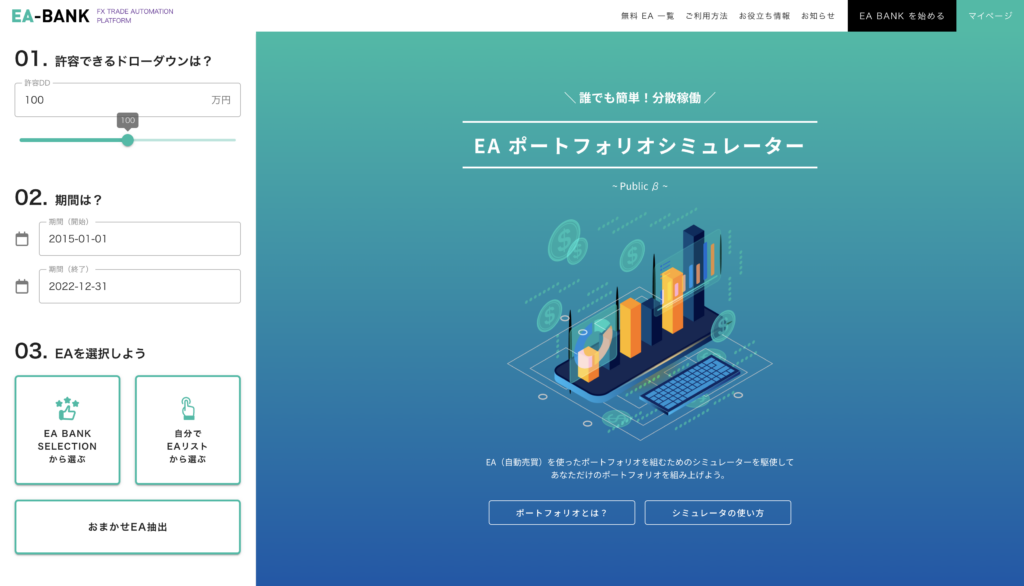
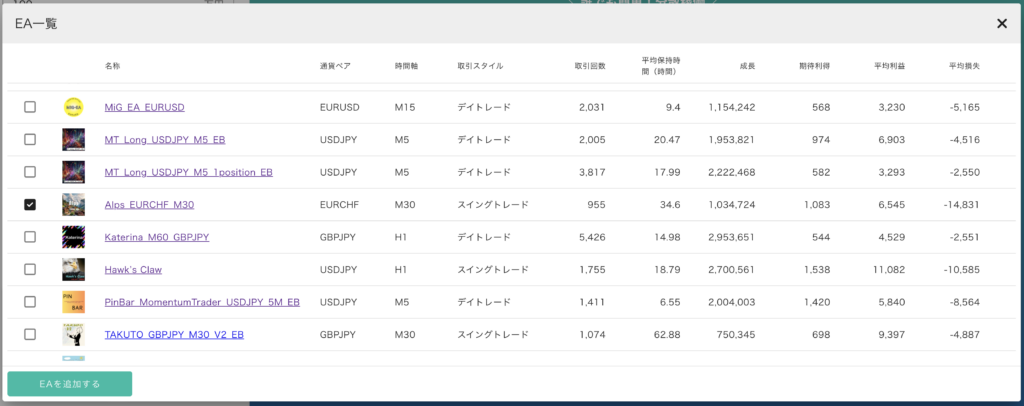
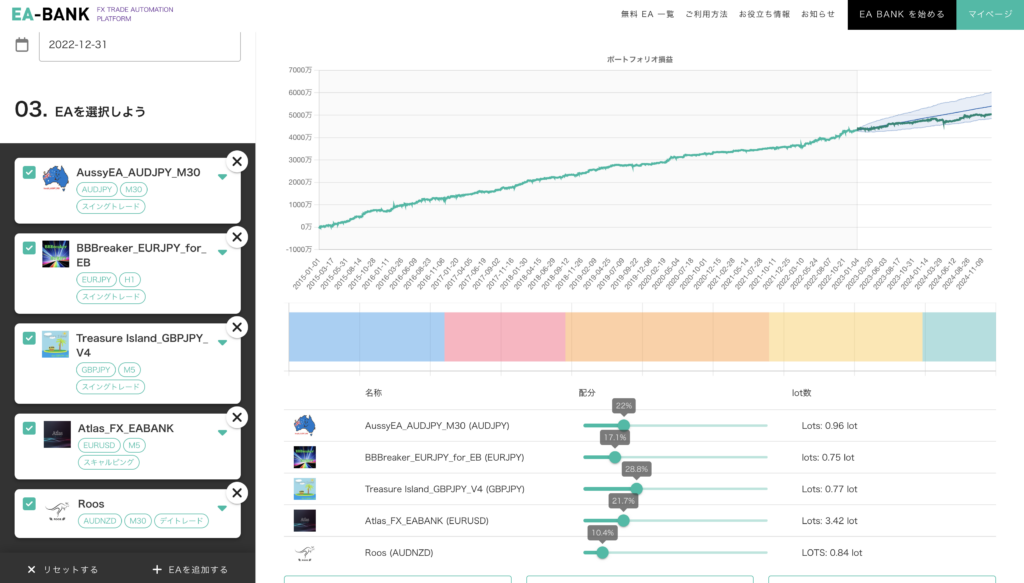
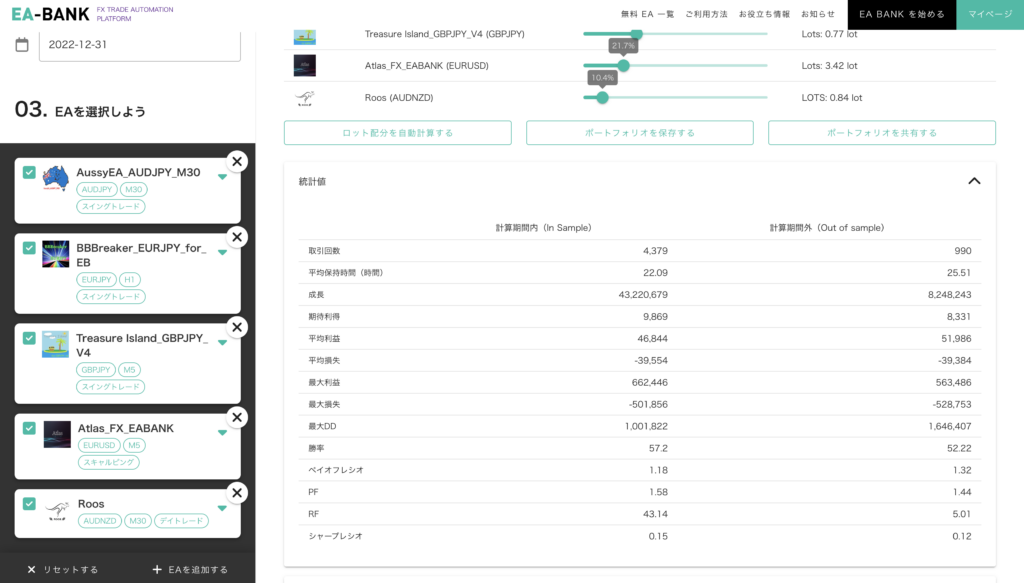
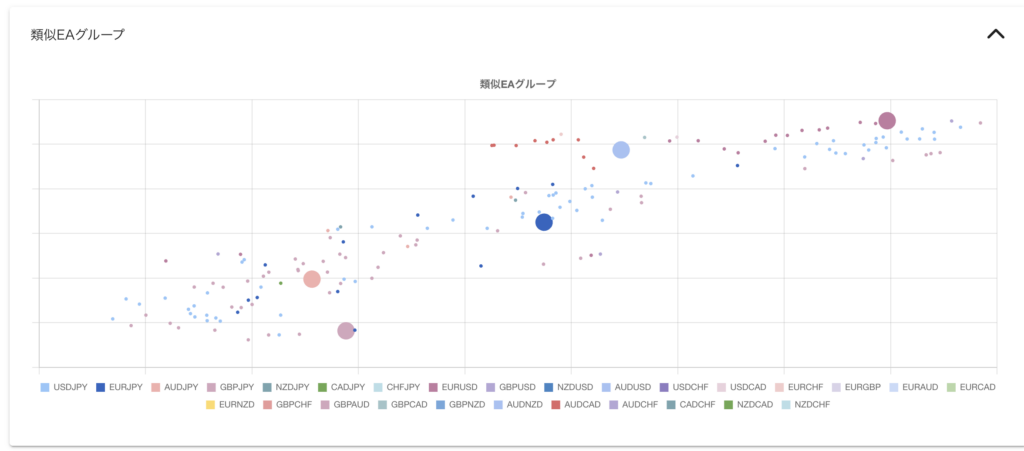
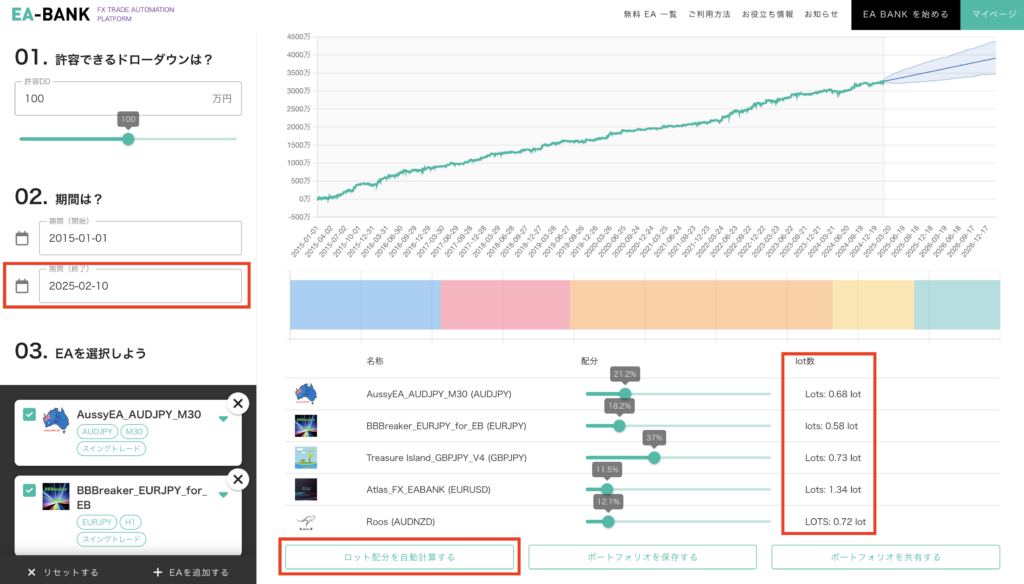
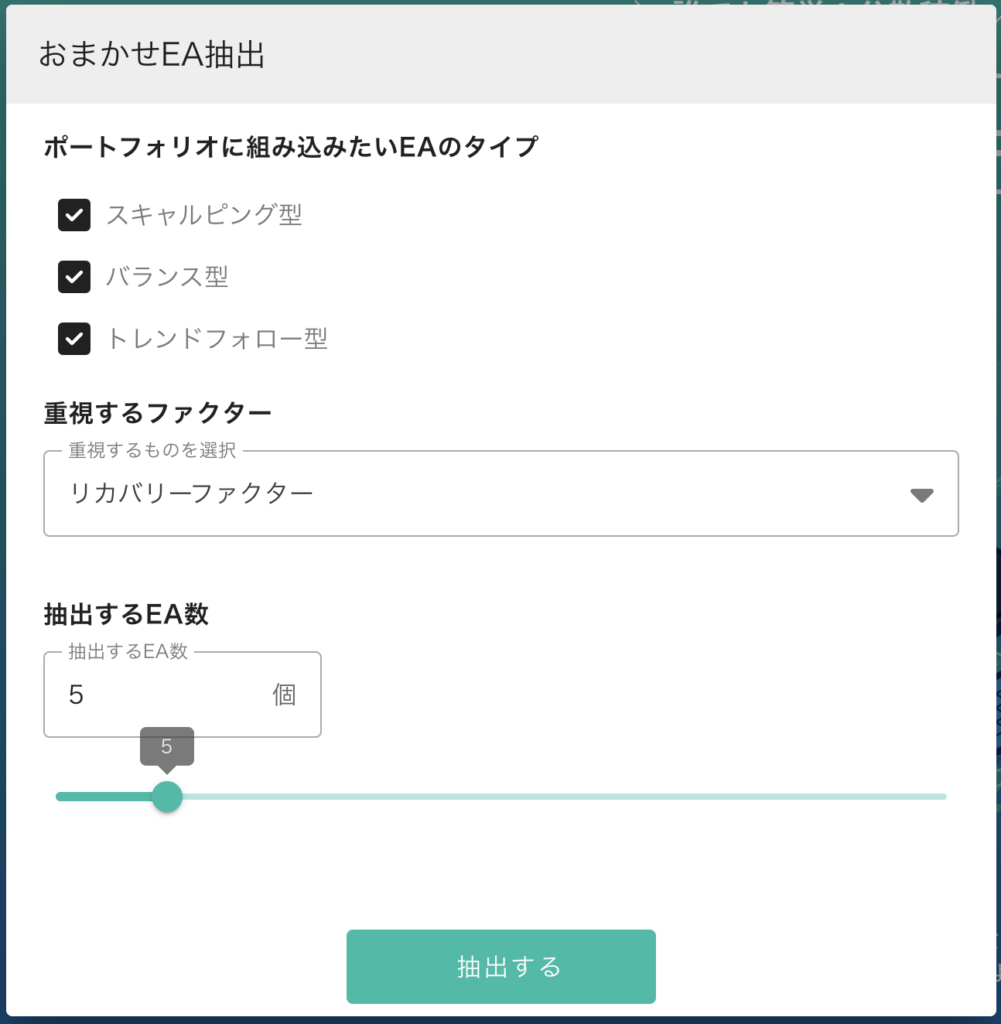
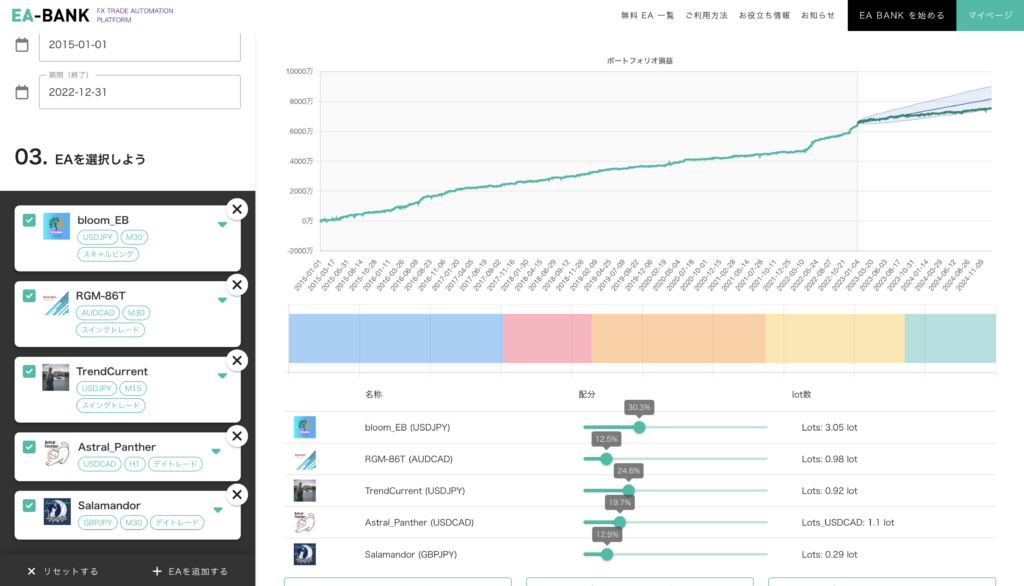
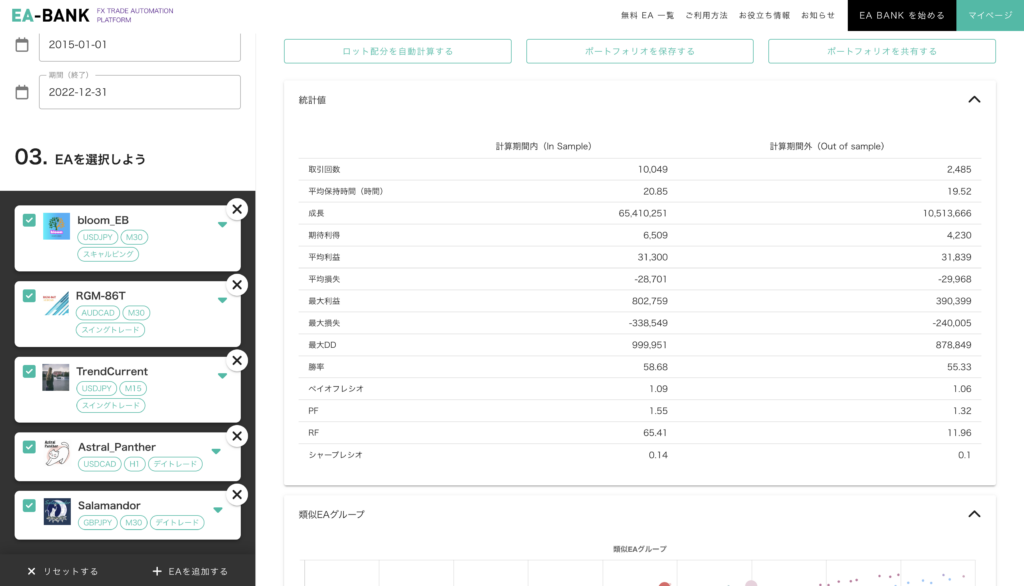
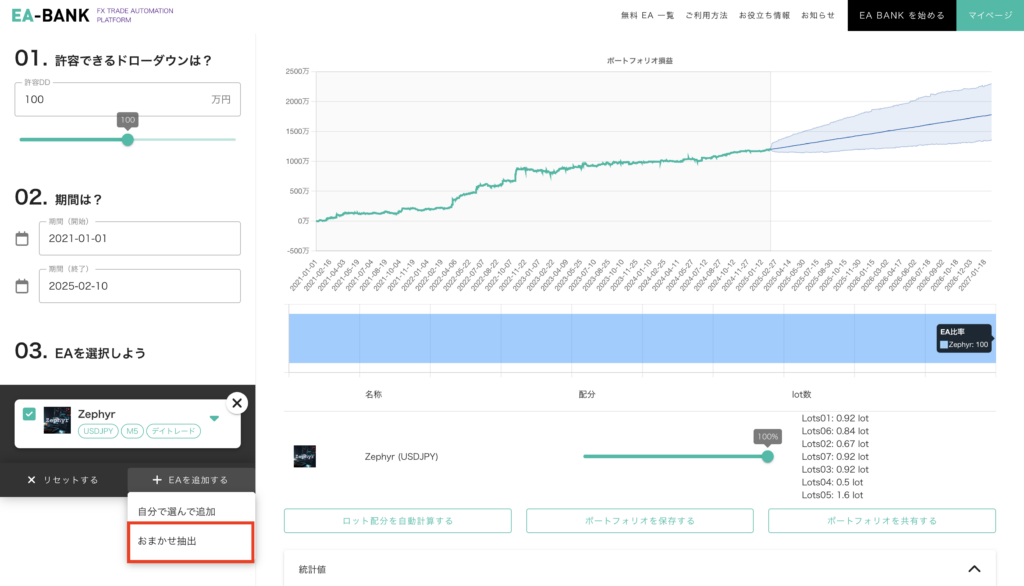
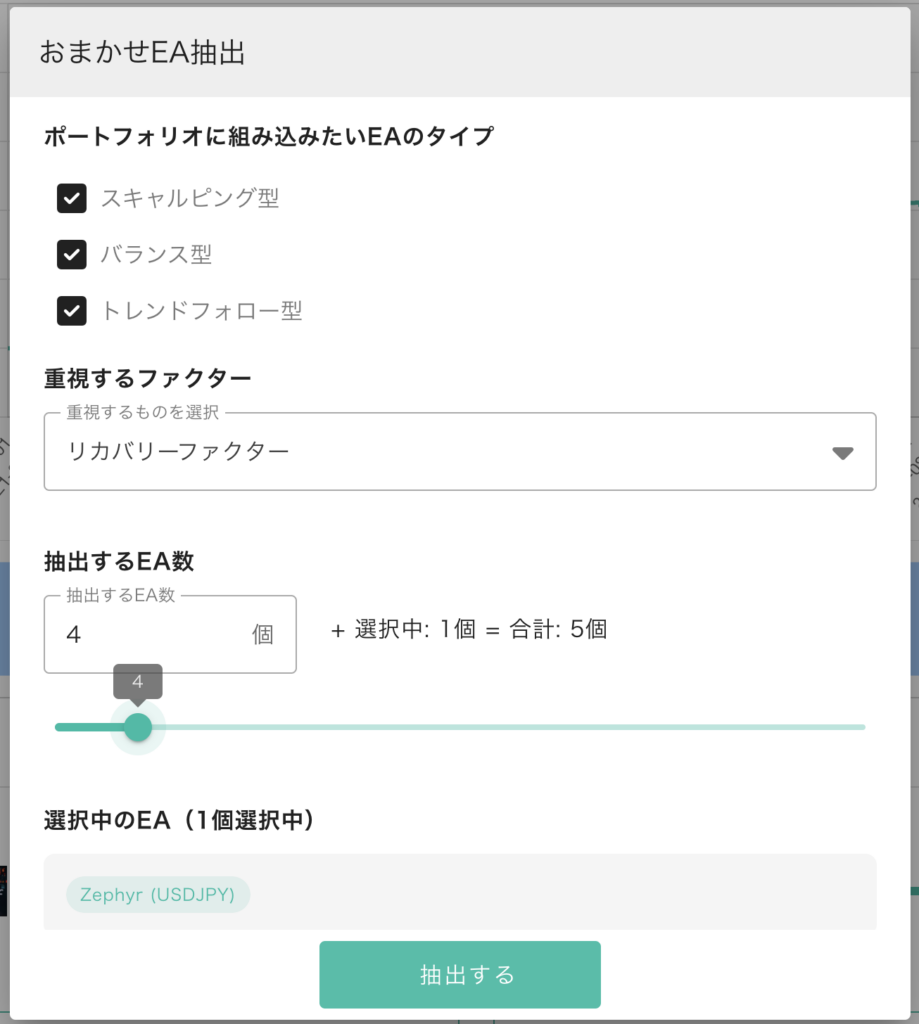
前回 まではポートフォリオシミュレータの使い方 について解説してきました。
今回の記事ではもう少し基本に立ち戻り、EA自体の分析について書いていきます。この記事の内容をある程度理解しておけば、厳しい審査がなされているEA-BANKだけでなく、玉石混交なEAが販売されているゴゴジャン などで勝てる確率が高そうなEAを見繕えるようになると思います。
分析を通して知りたいことと各分析の概要
分析の方向性がぶれないように、まずは知りたいことをまとめておきます。言うまでもなくEA分析を行う本質的な目的は 運用に値するEAかどうかを知ること 分析対象のEAの特性 多くのEAの中での分析対象EAの位置付け
前者では分析対象EAの成績にフォーカスしてEAの特性を分析し、後者では複数のEAを同じ切り口で見て比較したときに分析対象EAがどんなレベルにいるかを評価します。
まずは分析する項目の概略を説明し、その後に各節で項目の詳細を説明していきます。
説明全体は大変長くなっていますから、ご自身に必要な部分だけをピックアップして読むような使い方をしていただければと思います。
分析対象のEAの特性を知る
投資効率
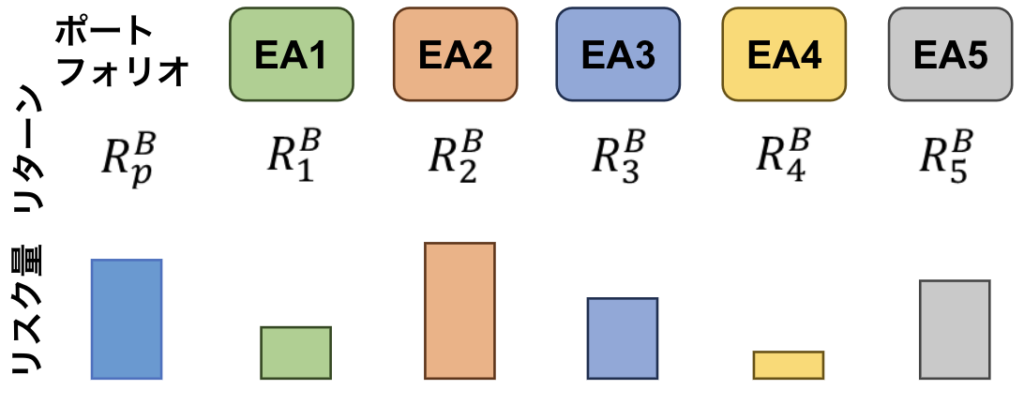
リスクに対するリターンを分析 します。投資効率は高ければ高いほどよく、この値が低い時点で使う選択肢から外れます。
リカバリーファクター (Recovery Factor, RF)シャープレシオ (Sharpe Ratio)ソルティノレシオ (Sortino Ratio)
利益と損失の特性
損益の特性を確認することでEAの戦略の特徴を把握 します。
勝率 (Winning Percentage, WP)ペイオフレシオ (Payoff Ratio, PR)期待利得 (Expected Payoff, EP)損益分布とそのスキュー (歪度, Skewness)
手仕舞い戦略の分析
EAを特徴づける大きな要因の1つが手仕舞いです。ポジションの保有期間と利益を横軸と縦軸に取った散布図を使い、手仕舞い戦略を分析 します。
バックテストからフォワード推移を予測する
EAのフォワードのエクイティカーブがバックテストどおりに推移しているかは、EAを評価する上で特に重要です。ただ、困ったことにここまでに出てきた指標は「時間」の要素が含まれておらず、時間あたりの取引回数の変化を評価できません。 バックテストではひと月に30回トレードがあったがフォワードではひと月5回しかない場合でも、指標が近ければ「順調」と評価されてしまいます。ここでは、バックテストから時間要素も含めてフォワードのエクイティカーブの予測推移を生成し、予測推移に対するフォワードの位置付けを評価します。
多くのEAの中での分析対象EAの位置付けを知る
損益特性と投資効率
EAの損益特性に対する投資効率を評価するために、横軸にリターンのスキュー(Skewness)、縦軸にソルティノレシオ(Sortino Ratio)を用いた散布図 を描きます。この散布図を用いて、同じような損益特性(スキュー)を持つEAに対する分析対象EAの投資効率の位置付けを分析 を行うとともに、異なる損益特性を持つEAを抽出 します。この分析を通して、似たEAの中で分析対象のEAがどの程度優れているかや、分散対象として相性の良いEAの候補を知ることができます。
勝率と損益特性
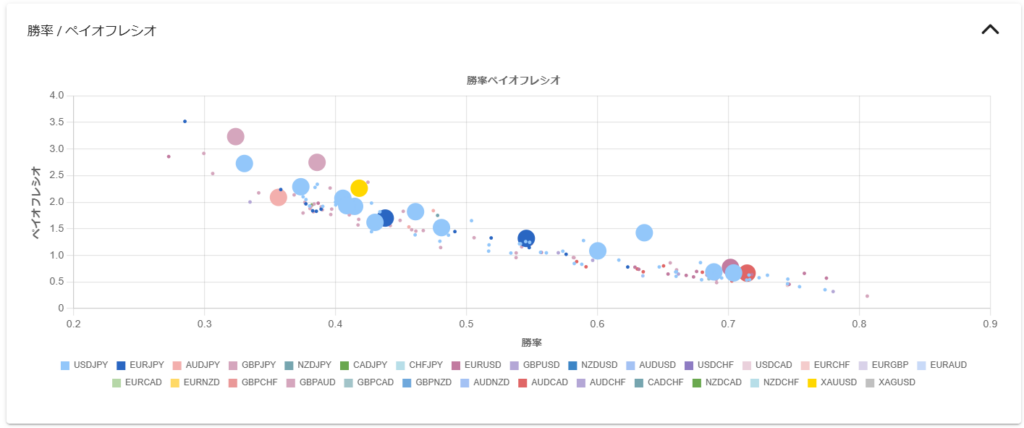
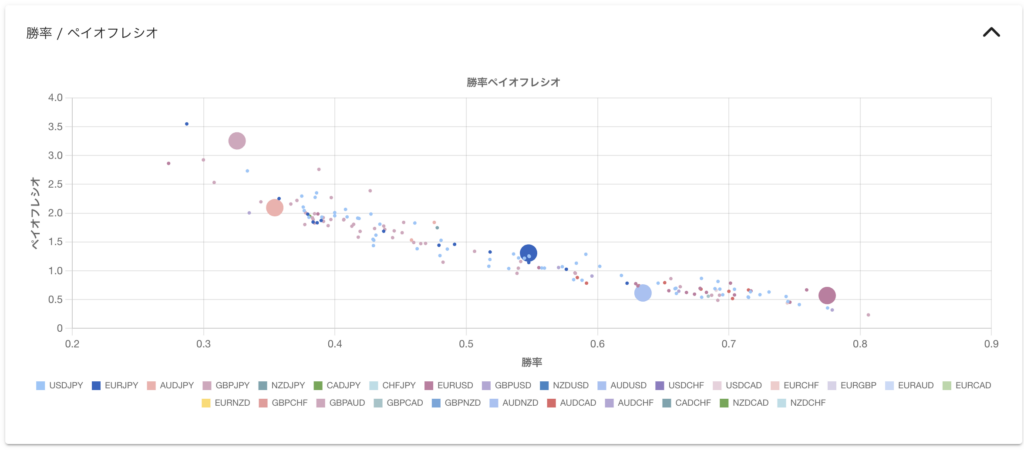
横軸に勝率(WP)、縦軸にペイオフレシオ(PR)を用いた散布図 を描くことで、EAのロジックの戦略を大まかに分類 できます。そして、WPとPRから計算する等価ラインを考慮して別のEAと比較するとこで行き過ぎた成績を持つEAでは無いことを確認するとともに、「損益特性と投資効率」と同様に分散対象として相性の良いEAの候補を抽出します 。
他のEAとのエクイティカーブの相関係数
分散投資による投資効率改善を目的として複数のEAでポートフォリオを組むうえで、他のEAとのエクイティカーブの相関係数を確認することは重要です。相関係数が極端に高いものを組合せても、ポートフォリオの必要証拠金額の増加に見合う投資効率改善が見込めない 場合があります。EA同士のエクイティカーブの相関係数を確認し、同時に動かすことで投資効率を改善できそうなEAの候補を抽出 します。
なお、すべてのEAに複利機能があるわけではないので、このブログにおいてはここまでの解析はすべて単利の結果に対して実施する点に注意してください。
詳しい説明
分析対象のEAの特性を知る
この節では、分析対象のEAの成績にフォーカスして分析をしていき、EAにお金を投入したときに高いリターンが見込めそうか(投資効率)、どういった戦略に基づくEAなのか(利益と損失の特性、手仕舞い戦略の分析) を把握していきます。
投資効率
この項ではリスクに対するリターンを分析 します。投資効率は高ければ投入した資金に対して大きなリターンが得られる可能性が高いですから、この分析は利益の期待値を見積もる最も重要な分析の一つです。用いる指標の特徴と何を見るために使うのか を順に説明していきます。
リカバリーファクター(Recovery Factor, RF)
リカバリーファクター (以降はRFと表記)は取ったリスクに対するリターンの比率を表す指標 全体の損益には注目しますが個々の損益は評価しない 点シャープレシオ(Sharp Ratio)やソルティノレシオ(Sortino Ratio)との違い です。
RFはリターンを「累積損益」、リスクを「最大の累積損失(Max Draw Down)」としています。累積損益を$CP$、最大の累積損失を$MDD$と表記すればRFは式(\ref{eq:rf})で計算できます。
\begin{eqnarray}
\label{eq:rf}
RF & = & \frac{CP}{MDD}
\end{eqnarray}
ただこのRFには1つ大きな問題があります。それは分子に累積損益を用いているために評価する期間の影響を受けてしまう ことです。10年間のテストのRFと1年間のテストのRFは前提が違うため直接比較できません。この問題はバックテスト・フォワード期間の異なる複数のEAを比較する際に表面化します。
対策はシンプルで、期間で正規化して「月あたり」や「年あたり」のRFを計算すれば良い です。このブログでは年あたりのRF(Yearly Recovery Factor, YRF)を用いる ことにします。YRFは式(\ref{eq:yrf})で計算します。
\begin{eqnarray} \label{eq:yrf} YRF & = & \frac{1}{\verb|Years|} \cdot \frac{CP}{MDD} \end{eqnarray}
ここで、$\verb|Years|$はテスト期間の年数を表します。10年なら$\verb|Years|=10$、5年6ヶ月なら$\verb|Years|=5.5$です。
シャープレシオ(Sharpe Ratio)
シャープレシオはRFと同様に取ったリスクに対するリターンの比率を表す指標ですが、RFとはリターンとリスクの定義が異なります 。シャープレシオのリターンは「損益率の平均値」、リスクは「損益率の標準偏差」 を使います。RFを全体の損益に着目した指標と表現するなら、シャープレシオは個々の損益に着目した指標 です。損益のブレが少なければ値が高くなるので、損益の安定性を評価する指標 と言っても良いと思います。
シャープレシオの計算式は式(\ref{eq:sharp})です。
\begin{eqnarray}
\label{eq:sharp}
SharpRatio & = & K \cdot \frac{\bar{r} – R_f}{\sigma_n}
\end{eqnarray}
\begin{eqnarray*}
\label{eq:sharp_R}
r_i & = & \left( \frac{p_i}{p_{i-1}} \right) \\
\bar{r} & = & \frac{1}{n} \sum^{n}_{i=1} r_i \\
\sigma_n & = & \sqrt{\frac{1}{n-1} \sum^{n}_{i=1} \left( r_i – \bar{r} \right)^2}
\end{eqnarray*}
ここで、$K$は調整定数で日次損益なら$K=\sqrt{252}$、週次評価なら$K=\sqrt{52}$です。$\bar{r}$は損益率の平均値、$p_i$はi本目の損益、$R_f$は無リスク金利(債権金利など)、$\sigma_n$は損益率の標準偏差を表します。このブログでは簡単のために$R_f=0$とします(超低金利の今、$R_f=0$で評価してもほとんど問題ありません)。
このシャープレシオを使うことで、全体を見るRFでは評価できなかった損益の安定性を評価 できます。
なお、式(\ref{eq:sharp})を見てわかる通り、シャープレシオは調整係数を掛けることで年あたりの値に変換するため「ポジションごとの損益」に対しては正しく計算できません 。加えて、日次損益で見ると取引がない日が多くなりすぎてしまい(10年で1000回トレードしても3日に1回程度)、月次損益で見ると荒く見すぎてしまいます。この理由から、このブログではEAに対してちょうどよい粒度の週次シャープレシオ を用いています。
もう一点注意すべき点として、シャープレシオは本来は資金量に対する割合でリスクをとるような複利運用を想定した指標 という点が挙げられます。常に証拠金の2%のリスクを取って4%のリターンを得るようなシステムを評価するならば損益率評価はマッチするのですが、EAのバックテストのように単利で長期に渡り評価することが多い場合は上記式の損益率$r$はだんだん小さくなってしまう問題があります。1年に1回あるかどうかの爆益のはずが、評価の最後に出現したがために前半の平均的な利益と大して変わらないと評価される ようでは、単利のEAを正しく損益を評価できるとは言えません。これを解決するために、このブログのEAの評価においてはシャープレシオを「損益率」ではなく「損益額」で計算する ことにします。
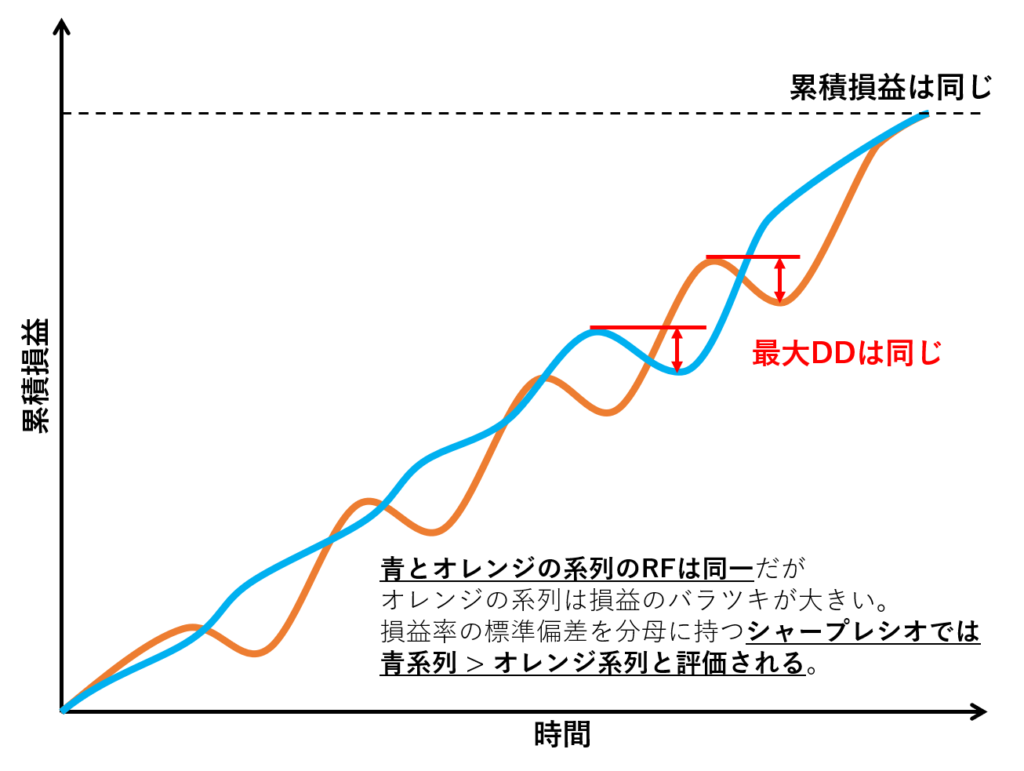
シャープレシオで評価できることをイメージするために例を挙げます。青系列 とオレンジ系列 の2つの損益線があるとします。2つの系列の累積損益も最大DDもまったく同じですが、青系列の大きなDDは最大DDの1度だけ なのに対し、オレンジ系列は定期的に大きなDDが生じている 点が異なります。運用するならば安定感がある青系列を採用したいところですが、2つの系列のRFは同一なのでRFでは判断できません。
こういう場合、損益のバラツキ(標準偏差)を考慮するシャープレシオが役立ちます。2つの系列の取引回数も同じだとすれば、シャープレシオの分子の損益率の平均値$\bar{r}$はほぼ同じになります。一方で分母の損益率の標準偏差$\sigma_n$は損益のブレの大きいオレンジ系列のほうが大きくなります。つまり、青系列のシャープレシオはオレンジ系列のそれより大きくなり、より安定して利益を上げられる(=投資効率が良い)と言えます 。
この例のように、RFだけでなくシャープレシオを見ることで損益の安定性の観点からEAを評価できます。
ソルティノレシオ(Sortino Ratio)
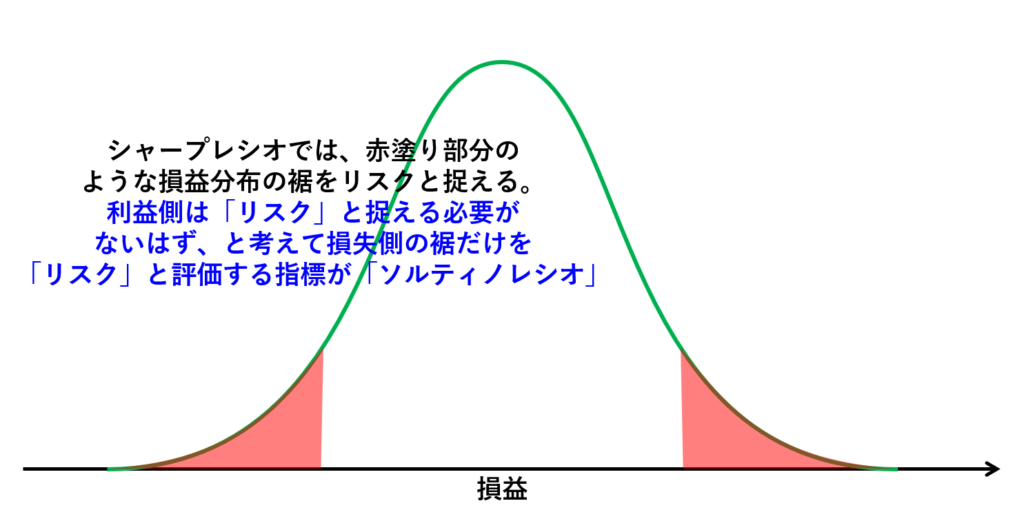
実は先ほど説明したシャープレシオには問題点があります。それは、シャープレシオはリスクを「損益率の標準偏差」で評価しているために、損失方向へのバラツキだけでなく利益方向へのバラツキもリスクと捉えている 点です。このために、トレンドフォロー戦略など大きな利益で複数の小さな損失をカバーする戦略のシャープレシオを過小に見積もってしまうことがあります。この問題に対応するために、「ソルティノレシオ」では標準偏差を「損失を出したリターン」だけで計算してリスクを評価 します。
ソルティノレシオは式(\ref{eq:sortino})で計算します。シャープレシオの計算式(\ref{eq:sharp})との変化点は分母の$\sigma_{down}$だけです。
\begin{eqnarray}
\label{eq:sortino}
SortinoRatio & = & K \cdot \frac{\bar{r} – R_f}{\sigma_{down}}
\end{eqnarray}
$\sigma_{down}$は、式(\ref{eq:sortino_sigma})のように損失だけに限定して標準偏差を計算しています。
\begin{eqnarray}
\nonumber
r_i & = & \left( \frac{p_i}{p_{i-1}} \right) \\
\nonumber
D_r & = & \{ r_i | r_i < 0 \} \\
\nonumber
\bar{x} & = & \frac{1}{N\left(D_r \right)} \sum_{x \in D_r} x \\
\label{eq:sortino_sigma}
\sigma_{down} & = & \sqrt{\frac{1}{N\left(D_r \right) – 1} \sum_{x \in D_r} \left( x – \bar{x} \right)^2}
\end{eqnarray}
ここで、$N \left( X \right) $ は集合$X$に含まれる要素数を表します。説明の関係上数式に$D_r$のような「集合」の考え方が出てきますが、これは「条件を満たす値の集まり」と考えていただければ問題ありません。ここでは「損益率が負の値の集まり」を意味します。
ソルティノレシオでは、損失がコントロールされて狭い範囲にまとまっているEAは良いと評価され、ときおりそれまでの利益を吹き飛ばすような損失を出すEAは悪いと評価されます。 定性的には、ナンピンや損失をコントロールしないスキャルピングは低く評価されやすく、損失をコントロールできるスキャルピングやトレンドフォローは高く評価されやすいと考えれば良いです。
利益と損失の特性
投資効率の項では、取ったリスクに対するリターンをを測る指標について見てきました。この項と次の「手仕舞い戦略の分析」の項ではEAの戦略を把握するための指標にフォーカス します。大切な資金を投入するEAについて深く理解するために、指標として計算した1つの数値を見るだけでなく、分布や散布図を確認することで指標からでは見えない傾向を把握していきます。
勝率 (Winning Percentage, WP)細かい説明はしません。全体の取引のうちの勝ちトレードの割合を表します。例えば勝率90%以上の極端な値の場合、フィルタロジックで過剰に負けトレードを排除している可能性があるため注意が必要 です。
勝ちトレード数を$N_{win}$、負けトレード数を$N_{lose}$とした場合、勝率$WP$は式(\ref{eq:winning_percentage})で定義できます。
\begin{eqnarray}
\label{eq:winning_percentage}
WP & = & \frac{N_{win}}{N_{win}+N_{lose}}
\end{eqnarray}
ペイオフレシオ (Payoff Ratio, PR)こちらも良く使われる指標なので詳しい説明はしません。ペイオフレシオはシステムの利益の平均値と損失の平均値の比 を指します。「リスクリワード」や「リスクリワードレシオ」と呼ばれることもあります。勝率とペイオフレシオはトレードオフの関係 にあることが多く、スキャルピングなどの高勝率を狙うEAだとペイオフレシオは1未満、トレンドフォローなどの高いペイオフレシオを狙うEAだと勝率は$50%$未満になりやすいといえます。
平均利益を$\bar{R}_{win}$、平均損失を$\bar{R}_{lose}$とした場合、ペイオフレシオ$PR$は式(\ref{eq:payoff_ratio})で定義できます。
\begin{eqnarray}
\label{eq:payoff_ratio}
PR & = & \frac{\bar{R}_{win}}{\bar{R}_{lose}}
\end{eqnarray}
期待利得 (Expected Payoff, EP)期待利得もよく使う指標なので概要の説明のみ行います。期待利得は1トレードで得られる利益の期待値 を指します。期待利得が小さすぎる場合、ボラティリティ上昇によるスプレッド拡大や通信遅延によるスリッページなどのコストに負けてしまい、フォワードで通用しない 可能性があります。期待利得が小さいEAを使う場合は動作環境には特に気を使う必要がある点に注意してください。
累積損益を$CR$、全トレード数を$N_{all}$とした場合、期待利得$EP$は式(\ref{eq:expected_payoff})で定義できます。また、ここまでに使った勝ちトレード数$N_{win}$、負けトレード数$N_{lose}$、平均利益$\bar{R}_{win}$、平均損失$\bar{R}_{lose}$を用いて式(\ref{eq:expected_payoff2})のようにも書けます。
\begin{eqnarray}
\label{eq:expected_payoff}
EP & = & \frac{CR}{N_{all}} \\
\label{eq:expected_payoff2}
& = & \frac{N_{win} \cdot \bar{R}_{win} + N_{lose} \cdot \bar{R}_{lose}}{N_{win} + N_{lose}}
\end{eqnarray}
損益分布とそのスキュー (歪度, Skewness)次に損益の特性を把握するために損益分布とそのスキュー を確認します。損益分布は、EAの分析においては損益のヒストグラムのことを指します。 損益のヒストグラムとは、損益額をある一定幅の区間に区切り、その区間に含まれるデータの数をカウントして横軸に損益額、縦軸にカウントしたデータ数をプロットした図のことです。
さてスキュー(Skewness)ですが、日本語では歪度といい、式(\ref{eq:skewness})で計算する分布の歪み具合(非対称性)を表す指標 です。
\begin{eqnarray}
\label{eq:skewness}
Skew & = & \frac{E\left[ \left( X – \mu \right)^3 \right]}{\sigma^3}
\end{eqnarray}
ここで、$X$はスキューを計算する集合の値、$\mu$は$X$の平均値、$\sigma$は$X$の標準偏差です。今回の場合は$X$は損益になります。Excelならば損益の列に対してSKEW関数を適用すれば計算できます。
軽く式を見てイメージを把握しておきましょう。分子に値と平均の差の3乗があります。3乗ということは、単なる差と比べると、符号はそのままですが平均に近いものはより小さく、平均から遠いものはより大きく評価されます。この性質があるので、平均に対して左右対称であればスキューはゼロ、スキャルピングのように利益側が密集(平均に近い)して損失側の裾が重い(平均から遠い)場合はマイナス、その反対でトレンドフォローのように利益側の裾が重く損失側が密集している場合はプラスになります。
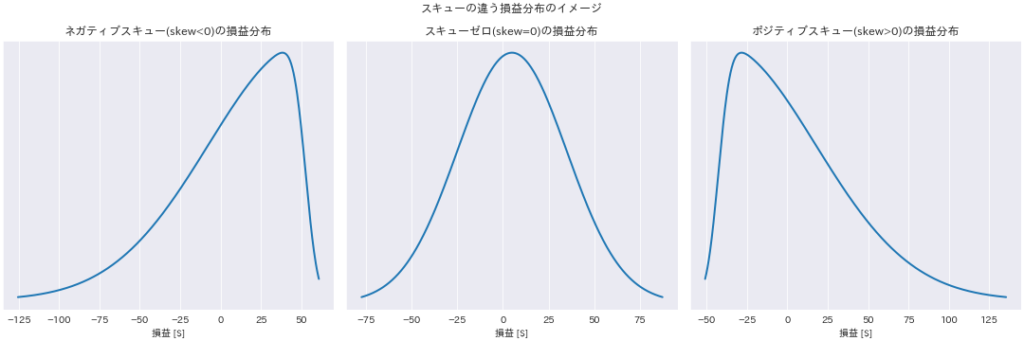
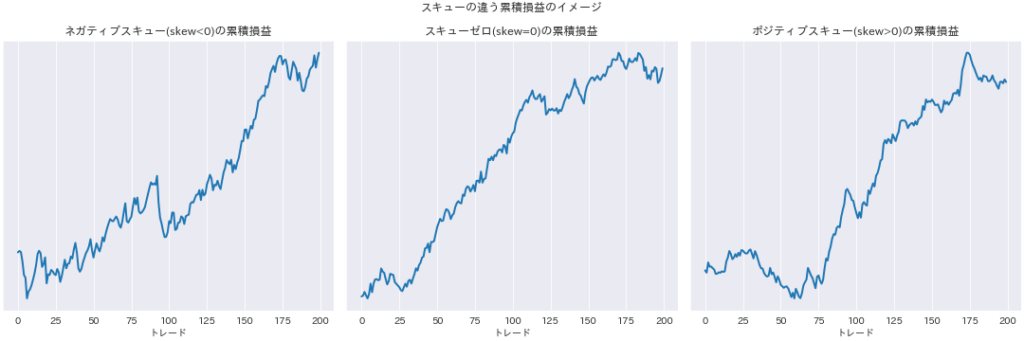
下の図は左から順に、スキューがマイナス(スキャルピング想定)、スキューがゼロ、スキューがプラス(トレンドフォロー想定)の損益分布のイメージです。
スキュー別損益分布イメージ。左からネガティブスキュー(スキャルピング)、ゼロスキュー、ポジティブスキュー(トレンドフォロー)。 ネガティブスキューの場合、利益は30ドル程度を高い勝率で稼ぐ一方、一撃で150ドル程度負けることもあるような分布になります。ネガティブスキューの損益分布を持つEAはいわゆるコツコツドカン型 です。スキャルピング系のEAによく現れる特徴です。下図(左)はネガティブスキューを持つEAの累積損益です。100トレード目辺りを見ると、ドローダウンに陥る際は勢いよく負け、じわじわと復活する様が見て取れると思います。
ポジティブスキューの損益分布を持つEAは、よく負けますが一度の勝ちでお釣りがくるくらいに勝つタイプ です。純粋なトレンドフォロー系EAに表れやすい特徴です。特性はネガティブスキューのちょうど反対です。累積損益(下図(右))の50トレード目前後を見ると、じわじわ負けて少数の勝ちで一気にドローダウンを抜け出す様が見て取れます。
スキュー別累積損益の例。左からネガティブスキュー(スキャルピング)、ゼロスキュー、ポジティブスキュー(トレンドフォロー)。期待利得はすべて同一。 注意して欲しいのは、スキューはポジティブだから良い、ネガティブだから悪い、というわけではない点 です。あくまでEAの特性を表す一つの指標と認識してください。
手仕舞い戦略の分析
ここでは、各トレードに対してポジションの保有時間を横軸、利益を縦軸に取った散布図を分析して手仕舞い戦略を考察 します。ランダムエントリーでも手仕舞い戦略さえ良ければトータルで利益を残せる場合があるほど、手仕舞い戦略はEAの利益獲得の手段として重要です。
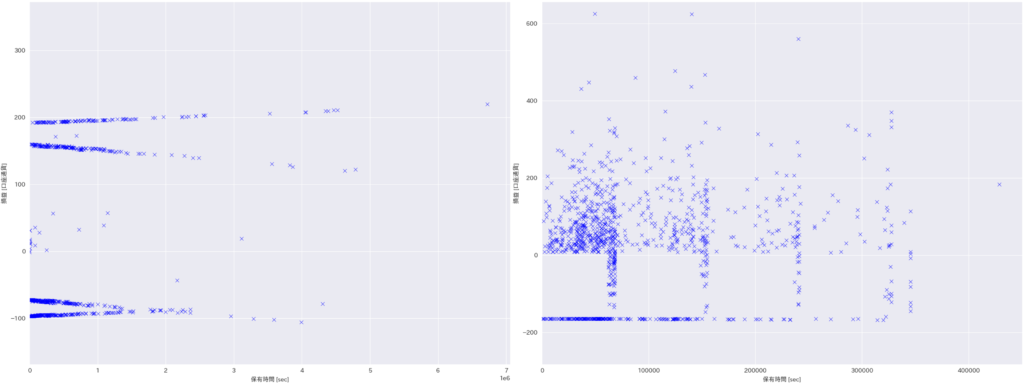
下図は、ある2つのEAの保有時間と損益の関係です。1つの点が1トレードに対応します。これらは保有時間と損益の関係に特徴的な傾向を持っていることが見て取れます。
左側のEAを見ると、ポジションの保有時間と損益の間に線形の関係が見て取れます。これは、時間と共に利益目標・損切り位置を変化させるロジック、もしくはスワップが特に大きい通貨ペアを扱うEAに現れる特徴 です。仮に前者だとすると、このEAは時間依存の利益目標・損切り位置設定ロジックをそれぞれ2種類持っていることになりたいへん興味深いです。これを少し踏み込んで考えると、このEA特有の環境認識を行い、時間とともにリスクを下げるほうが良いのか、それとも一方向に動くと見てより大きな利益を取りに行くほうが良いのかを判断しているのかもしれません。
右側のEAは、同じ間隔で4本縦線が生じているのが見て取れます。これは確定足で決済が入るEAによく出現する傾向 です。加えて、下方の損切りラインから損益ゼロの間に確定足決済を除いてトレードがほとんど存在していません。この傾向は、一定の利益が出たときに損切りをブレークイーブンに持ち上げると出現 します。ブレークイーブンより上の損益ではトレードが散っており損切りラインのようなまとまった横線がないので、指値決済は行わず、おそらくロジック決済とトレーリングストップを主としているのだと読み取れます。
このように、手仕舞いでよく考慮される「ポジション保有時間」と「損益」を組合せて表示することで、手仕舞い戦略を詳細に分析して理解できます 。
バックテストからフォワード推移を予測する
EAを評価する上でフォワードがバックテストどおりに推移しているかは特に重要にもかかわらず、ここまでに出てきた指標は「時間」の要素が含まないために時間あたりの取引回数の変化を評価できません 。バックテストではひと月に30回トレードがあったがフォワードではひと月5回しかない場合でも、指標が近ければ「順調」と評価されてしまいます。
この「バックテストからフォワード推移を予測する」では、バックテストのトレードの時間的・損益的性質を維持したまま擬似的なトレードを発生させたときに、予測される推移の分布がどうなるかを可視化 します。
もう少し噛み砕いて説明します。もしフォワード結果がこの範囲から外れていれば、全体の5%しか起こらないような状態、つまり異常な状態にある可能性が高い 、と言えます。フォワードが下側(97.5%)より下回って推移していればバックテスト通りに推移していない と言って良いと思います。
フォワード推移予測には別の使い方もあります。 このEAはここから平均に回帰するように連勝する可能性がありますから、まだこのEAを運用していないならば運用の始めどき です。反対に、上側(2.5%)より上回って推移していれば近々平均に回帰するようなドローダウンが発生する恐れがありますから、いったん運用を停止して様子を見ると良い かもしれません。当然外れることもあり確実ではありませんが、このようにEAの運用判断にも使えます。
では、具体的なやり方です。単純な方法として「ブートストラップ法」を使うことができます。 ブートストラップ法は、限られたデータから構成される系列を使って、もっとたくさんのデータがあるときの平均値がどの範囲にありそうかをを推定する手法です。そのために、データ系列からランダムに何回もサンプリング(リサンプリングといいます)して、似ている別のデータ系列を何本も作成してそれぞれの平均値を出し、作成した平均値の分布を作成する手順を踏みます 。EA分析に当てはめれば、「バックテストのトレードから重複を許してランダムに100トレード抽出する」ことを1試行として、1000試行実施するイメージです。
ここでは、ブートストラップ法を使えばリサンプリングによってバックテストから将来の推移を何本も作成できる という点にフォーカスしてフォワード推移予測に用いることにします。
実際のEA分析で使っている方法では、バックテストで出てこないトレードを生成するためにもう少し難しいことをやっていますが、本質的にやっていることは変わりません。
バックテストのトレードのうち、再現している性質は以下の3つです。
損益 ポジション保有時間 = CloseTime[t] – OpenTime[t]建玉時の、1つ前の建玉時刻からの経過時間 = OpenTime[t] – OpenTime[t-1]
この3つを再現することで、バックテストからトレードの時間的性質を考慮して将来の推移予測が行なえます。 バックテストのトレードに対して上記3つの値を計算しておけば、Excelでもブートストラップ法でフォワード推移予測が行えます(詳しくは説明しません)。
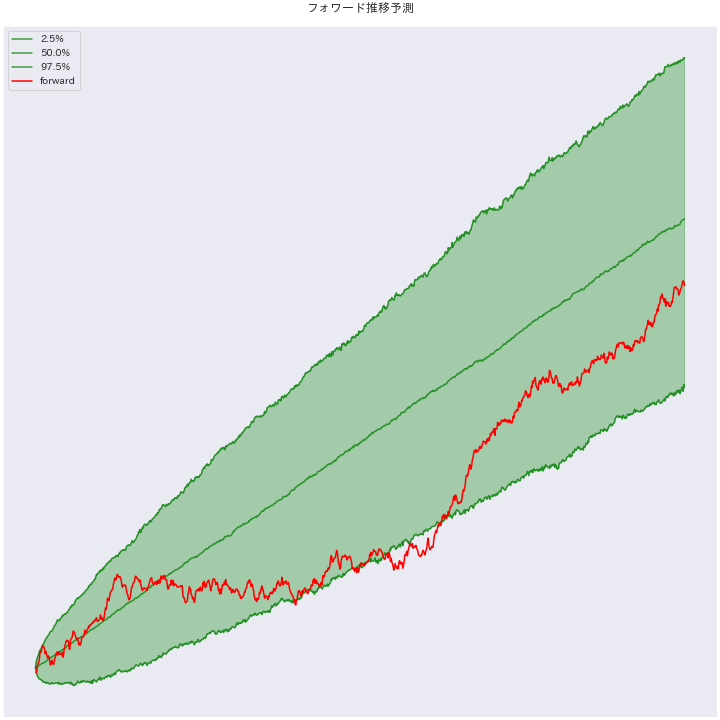
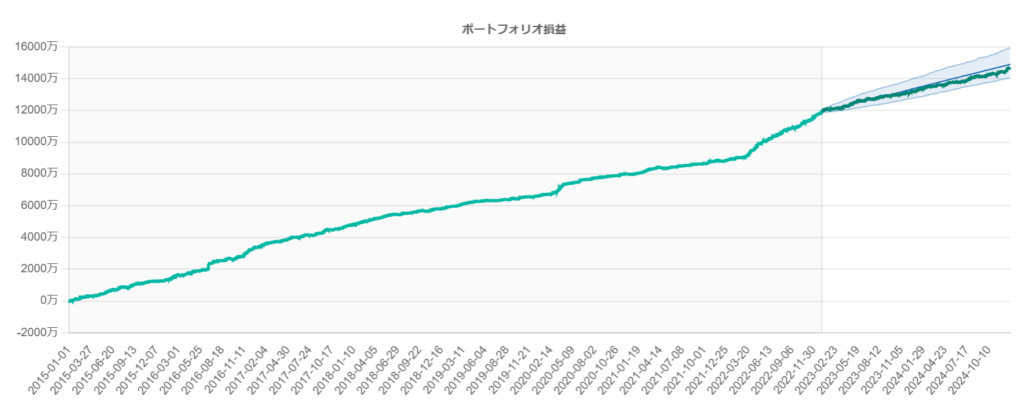
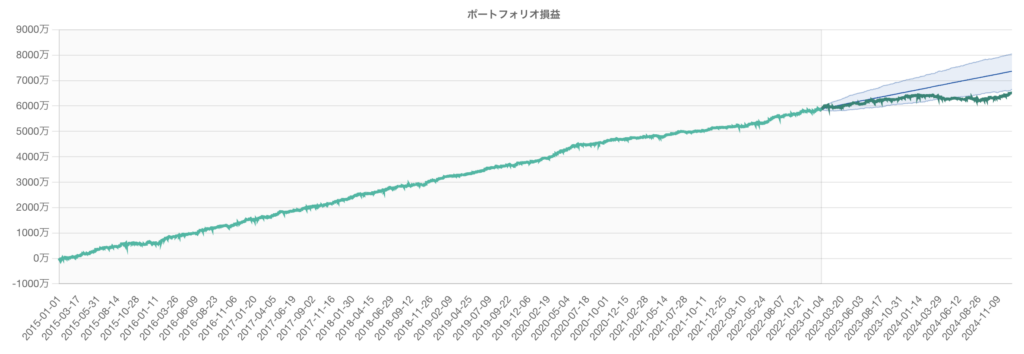
下図は、この方法でフォワード推移予測を生成した際のイメージです。
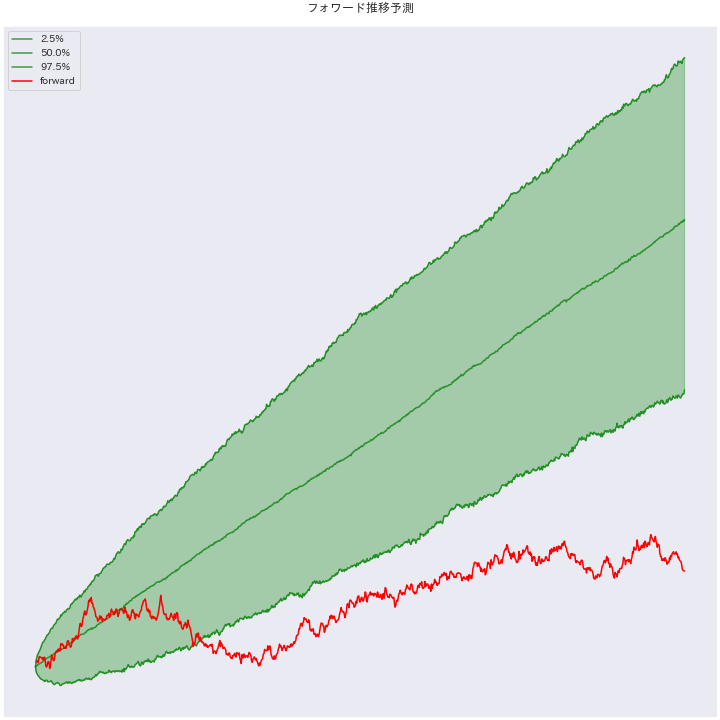
緑色の背景の範囲にバックテストから予測したエクイティカーブの期待値が含まれる確率が95%の範囲です。先ほど説明したとおり、この範囲から外れた場合は普通ではない状態です。左図はフォワードがバックテストどおりに推移している例 です。真ん中あたりでフォワードが下側を外れていますが、バックテストどおりに従っていれば平均に回帰する可能性が高い ですから、このタイミングでEAの稼働を始めれば大きく勝てる可能性があります。
一方、右側はもはやフォワードが機能していない例 です。常に下限を下回って推移しており、もう95%区間に回帰することはなさそうで稼働する意味のないEAです。稼働後しばらくは範囲内を推移することがほとんどで見分けがつかないことも多いですが、数ヶ月あれば概ね判断できるはずです。
さいごに、複数通貨をトレードするEAの場合、この分析はまず通貨ごとに行い各通貨での結果を把握したうえで、複数通貨での結果を分析 するようにしてください。通常、複数通貨でのトレード結果を集約した場合はリターンの分散が小さくなる傾向があり信頼区間の幅が小さく出やすい(分散効果)ため、EAの特性を見誤る可能性があります。また、通貨ごとにフォワード推移が異なるため、すべての結果をまとめると通貨ごとの推移の良し悪しがわからないことが理由です。
多くのEAの中での分析対象EAの位置付けを知る
「分析対象のEAの特性を知る」、そして「バックテストからフォワード推移を予測する」では1つのEAの特性を見てきました。この「多くのEAの中での分析対象EAの位置付けを知る」では、名前の通り複数のEAに対して分析対象のEAを比較していきます。そして、位置付けを知ることを通して分析対象とは異なる特性を持つEAを抽出し、同時に動かすことで分散効果が得られやすいEAを確認します。
損益特性と投資効率
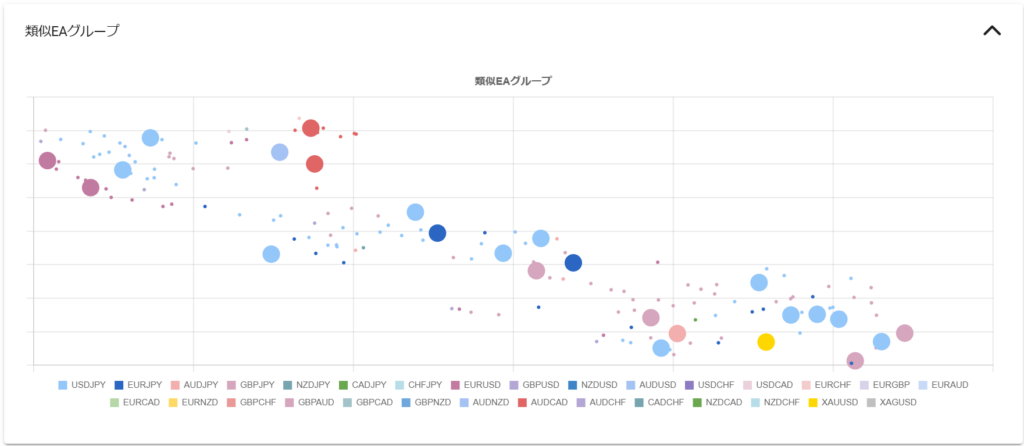
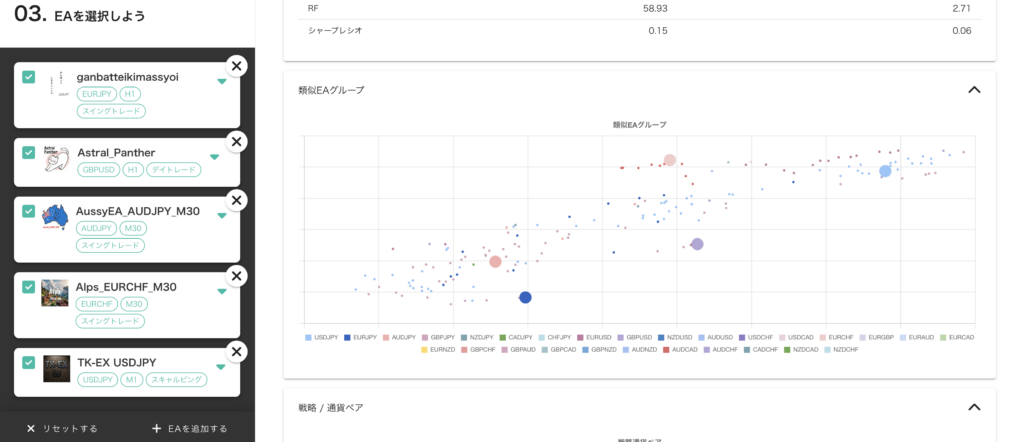
ここでは、同じような損益特性を持つEAの中で分析対象のEAの投資効率がどの程度か、他のEAと差別化できているのかを知ることで、相性の良い分散対象候補を見つける ために、EAの損益特性を表すスキューと投資効率を表すソルティノレシオ を用いて分析していきます。2つの指標を組合せて分析することで、1つの指標を見るだけではわからないEAの特性が見えてきます 。
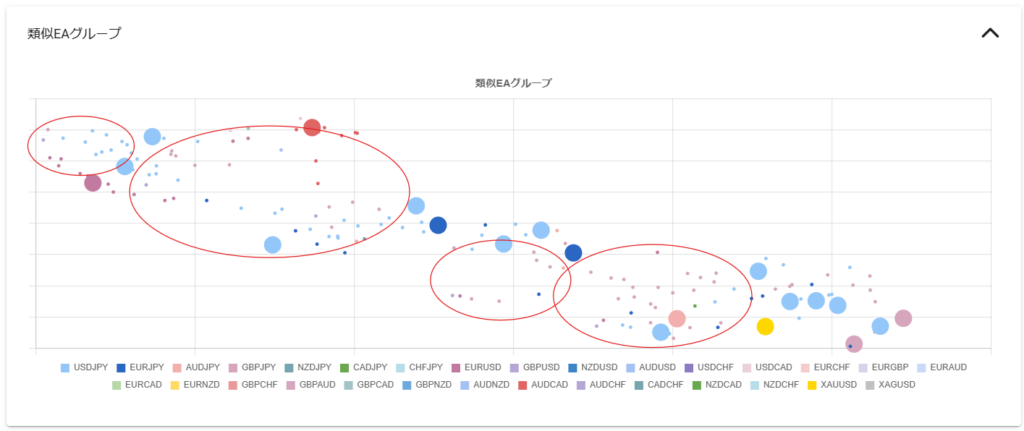
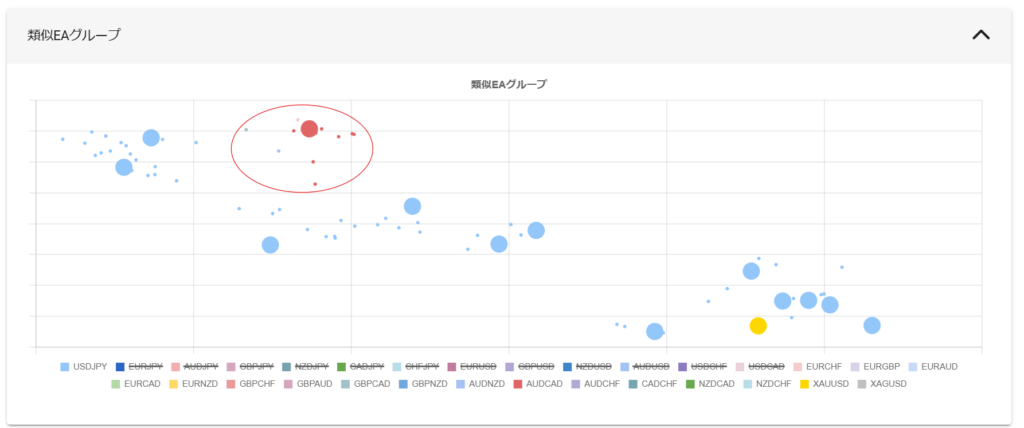
以下の図は横軸にスキュー、縦軸にソルティノレシオを取りEAをプロットした散布図です。ソルティノレシオは週次の損益に対して計算 しています。横軸のスキューは損益特性を表しますから、分析対象のEAに近いスキューを持つEAは同じような勝ち方/負け方をする似たEA と言えます。
以下の図はインタラクティブレイアウトを採用しているため、PCやスマホの横置きなど横長の画面での閲覧を推奨します。
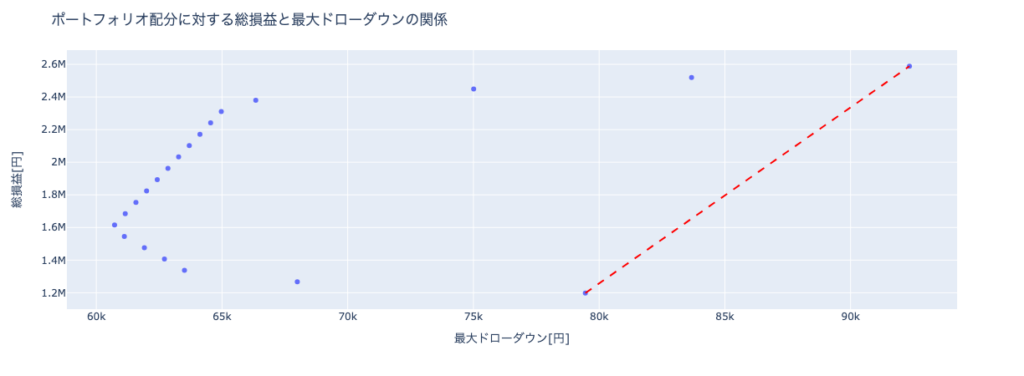
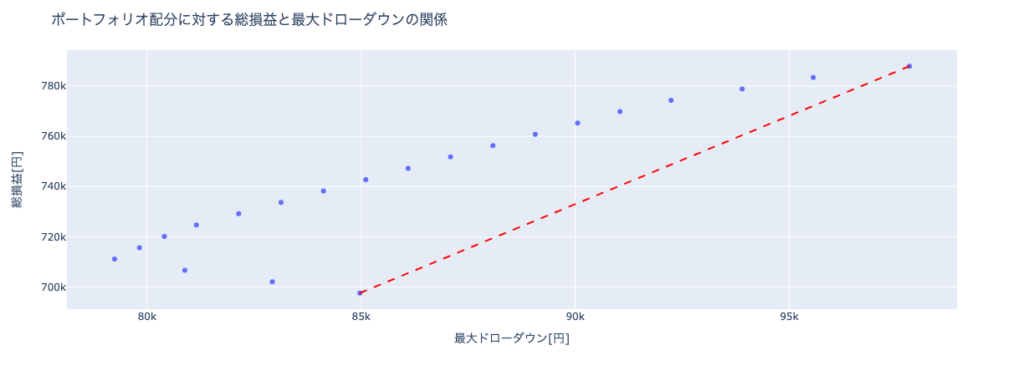
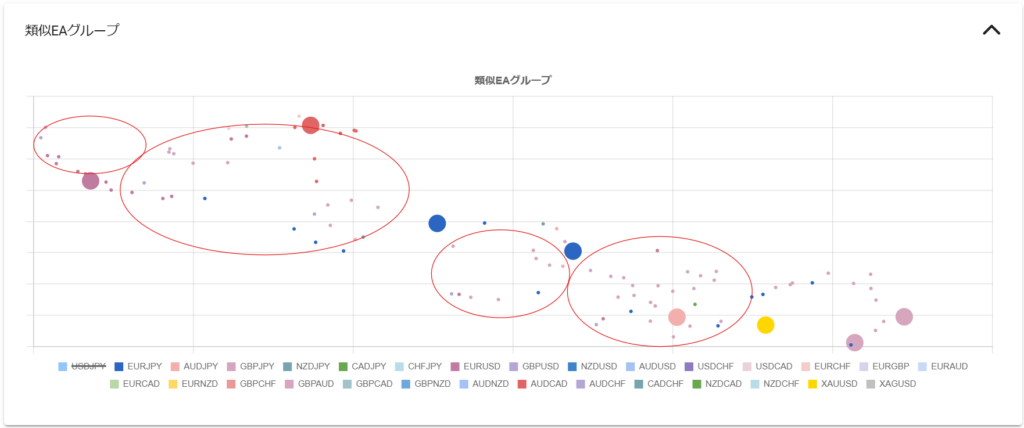
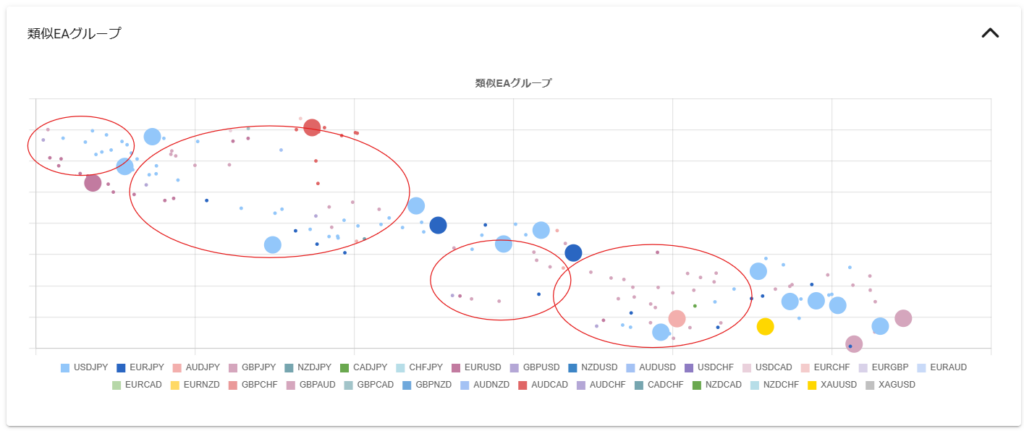
例えば、スキューが $-1$ 周辺の青色の点KonokaSystem_USDJPY_M5 を分析対象とするならば、比較対象は近いスキューを持つMBTradingSystem 、ED1 、Power_Scal 、Beatrice DELTA2 、Rhino_WinMode 、CROCUS_EURJPY 、Cradle 、ロンドンは午前7時 あたりになります。MBTradingSystem は頭ひとつどころかほかを突き放したソルティノレシオを示していますが、公式のバックテスト期間がわずか4年間のため、この時点では分析からは除外するのが懸命 です。分析に含めるのならば十分な期間のバックテストを実施した後が良いでしょう。KonokaSystem_USDJPY_M5 を類似のEAと比較すると、KonokaSystem_USDJPY_M5は頭一つ抜けたソルティノレシオを持ち、より効率的な投資対象 だとわかります。もちろん「バックテストからフォワード推移を予測する」で分析したフォワード推移が順調であることが大前提 になります。ただ注意して欲しいのは、これらの中でKonokaSystem_USDJPY_M5 だけを使えば良い、と言っているわけではない 点です。EAでポートフォリオを組む目的はロジックや投資対象を分散することで1EAだけを動かす場合よりリスクを減らして多くの利益を得ること ですから、取引通貨や時間足が異なれば分散対象になり得ます。EURUSD M5の ロンドンは午前7時 と、EURJPY H1のCradle と、USDJPY H1のRhino_WinMode を分散対象に使っても良いのです。「頭一つ抜けた」というのはあくまで同じ投資対象(取引通貨、時間足)の中の話です。
ではこのKonokaSystem_USDJPY_M5 と相性の良い分散対象のEAはどれでしょうか。答えは上で書いたとおり「ロジックや投資対象を分散 」できる相手、つまりスキューが異なり、取引通貨や時間足が異なるEA です。今回は大きなネガティブスキューを持つMultiLogicShot_EA や上がり3ハロン 、レアなポジティブスキューEAのLegato USDJPY ・梓弓 USDJPY ・梓弓 EURUSD ・Power_of_Japan あたりが候補となります。Legato USDJPY や梓弓 USDJPY は投資対象が重複しますから、スキューゼロあたりのRhino_ProfitMode やRECOBA Triple Swing M5 、3本の矢 も良い分散対象候補になります。
このように、損益特性と投資効率の軸でEAを分析することで、特性が良く似たEAの中での分析対象EAの投資効率の位置付け がわかります。また、損益特性の軸上で離れた位置のEAを見つけることで、ポートフォリオを組んだ際にリスク低減が期待できるEAの候補を抽出 できます。
勝率と損益特性
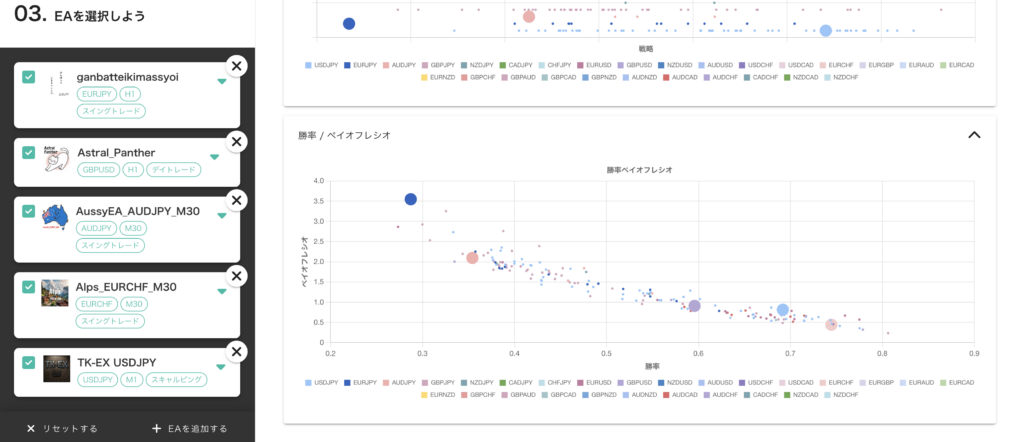
ここでは、EAの特性を表す勝率とペイオフレシオの2つを使うことでEAの戦略を大まかに分類 します。そして、勝率とペイオフレシオから等価ライン(プロフィットファクター)を計算してグラフ上に描くことで、特性の異なるEAを比較する基準 を作成します。
下図は横軸に勝率(Winning Percentage)、縦軸にペイオフレシオ(Payoff Ratio)を取った散布図です。3本のラインはプロフィットファクター(Profit Factor, PF)が$1, 2, 3$のラインです。プロフィットファクター$PF$は総利益÷総損失で計算でき、式(\ref{eq:winning_percentage})の勝率$WP=\frac{N_{win}}{N_{win} + N_{lose}}$と式(\ref{eq:payoff_ratio})のペイオフレシオ$PR=\frac{\bar{R}_{win}}{\bar{R}_{lose}}$を使って式(\ref{eq:PF-PR-WP})と表現できます。
\begin{eqnarray}
\nonumber
PF & = & \frac{\bar{R}_{win} \cdot N_{win}}{\bar{R}_{lose} \cdot N_{lose}} \\
\nonumber
& = & \frac{\bar{R}_{win}}{\bar{R}_{lose}} \cdot \frac{N_{win}}{N_{lose}} \\
\nonumber
& = & PR \cdot \frac{ \frac{N_{win}}{N_{win} + N_{lose}} }{ \frac{N_{lose}}{N_{win} + N_{lose}} } \\
\label{eq:PF-PR-WP}
& = & PR \cdot \frac{ WP }{ 1 – WP }
\end{eqnarray}
あとは$PF=PR \cdot \frac{ WP }{ 1 – WP }=1,2,3$となる$WP$と$PR$の組を計算すれば、勝率とペイオフレシオのグラフ上にPFの線を引けます。
※このグラフは横長の画面での閲覧推奨です。
このグラフ上では、スキャルピングのような高勝率低PR型のEAは右下に、トレンドフォローのような低勝率高PR型のEAは左上に配置 されます。そして、総損失に対する総利益が大きい(PFが高い)EAは右上 に寄っていきます。ここで注意して欲しいのは「PFが高い=優れたEA」ではない という点です。特に高勝率型EAの場合、もともと損失を出す取引の総数が少ないため、強くフィルタをかけ負け取引を排除するだけで簡単にPFは上がります 。このようなEAはフォワードでも一時的に勝てるかもしれませんが、バックテストに出現しない値動きが起きたときにフィルタが機能せず、莫大な損失を計上して一撃退場になりかねません。少なくとも長く勝ち続けることはできない でしょう。勝率60~70%を超えており、かつPFが2を超えるようなEAには注意が必要 です。もちろん優れたアルファを見つけてEAとして実装した例もありますから、EAのロジックを含めて精査したうえでの判断が必要です。
このグラフにおける戦略の分類方法ですが、基本は「近くにいるものは似ている」という考え方です。同じような勝率、勝ち負けの損益比率のEAは似たロジックを採用している 、というスタンスです。例外もありますが、勝率が0.6を超えてPRが1.0を下回るようなEAはほとんどがスキャル型と言えますし、逆にPRが1.0を超えてくるEAはトレンドフォロー型と言えます。スキャル型の極端な例はMultiLogicShot_EA と上がり3ハロン 、トレンドフォロー型の例はLegato USDJPY です。前者は勝率が9割を超える代わりにPRが0.1前半しかない毎回勝つことを重視したロジックであるのに対し、後者はPRが2に近い代わりに勝率が4割の、小さく負け続ける中で大きな勝ちを狙うロジックです。この例から明らかなように、勝率とPRが明らかに異なるEAはロジックの狙いそのものも異なる可能性が高く、同時に運用することで高い分散効果を得られると期待できます 。
一方で勝率0.6~0.7辺りをみると、多くのEAが集まっています。これらのEAは今回の勝率とPRという切り口で見ると同じような特性を持つよく似たEA であると言えます。これらのEAはすべて小さく勝って大きく負けるタイプです。そのため、2019年のフラッシュクラッシュや2020年のコロナショックなどの想定外の大相場が来たとき、すべてのEAがまとめて大きく負ける可能性があります。 上記ショックのような極端な動きをする“クライシス” と呼ばれる相場では、平時のリターンの相関が低いとしても同じようなロジックを持つEAの相関は高くなりやすい です。理由は様々ありますが、クライシス相場ではどの通貨・時間足でも一様にボラティリティが高くなり、一方向に協調して変動することが増えることがひとつの理由だと考えられます。ただ注意して欲しいのは、この中の1つだけを動かせと言っている訳ではない 点です。同種のロジックでも取引通貨や時間足が異なるEAでポートフォリオを組めば分散効果は得られます。避けるべきは、同種のロジック”だけ”でポートフォリオを組みクライシスで退場に追い込まれること です。様々なロジックに投資対象を分散し、かつ同種のロジックでも異なるいくつかの対象に分散することが、もっともリスクを減らせるポートフォリオの組み方のひとつです。
まとめると、この分析で把握すべきことは以下の2点です。
同時稼働は注意すべき、分析対象のEAとよく似た特性を持つEA 良い分散対象となる、全く異なる特性を持つEA
これらを把握することで、分析対象のEAと比べる対象となるEAがわかり、同時にポートフォリオを組む候補を見つけられます。
他のEAとのエクイティカーブの相関係数
ここまでは目視で直感的にわかる分析を行ってきました。ここではもう少し数値的にEA同士の関係性を見ていきます。具体的には、タイトル通り「EA同士のエクイティカーブの相関係数」を計算することでEA同士の似ている度合いを判断 します。相関係数には式(\ref{eq:correlation})で表現されるピアソンの積率相関係数$COR$を用います。一般に使われる相関係数です。
\begin{eqnarray}
ここで、$x_i, y_i$ は相関係数を計算する2つの系列$X, Y$の値、$\bar{x}, \bar{y}$は系列${x_i}, {y_i}$の平均値です。相関係数は系列$X, Y$の共分散$cov\left(X,Y\right)$と標準偏差$\sigma_X, \sigma_Y$を用いて式(\ref{eq:correlation2})と書くこともできます。
\begin{eqnarray}
分析を行ううえで知っておくべき相関係数の特徴を説明しておきます。相関係数は2つの系列の間の「直線的な」関係性を測定する指標 です。単利のEAのリターン同士の関係性は正しく測定できますが、単利と複利のリターンの組み合わせやリスク割合が異なる複利のリターンの組み合わせは2つの系列の関係が「非線形、曲線的」になるので、相関係数では正しく関係性を測定できません 。単利と複利の組み合わせはそもそもリスクの取り方の土俵が違うので通常は比較しません。複利同士の比較では対数変化率$\log\left( p_i / p_{i-1} \right)$を使って比較することで、単利同士を変化額$\left( p_i – p_{i-1} \right)$で比較する場合と同じように比較できます。
本ブログでのEAのエクイティカーブの相関係数は、週次で集計したエクイティカーブの変化額をもとに算出 します。週次を使う理由ですが、EAの運用判断は日ごとには行わず最低でも週ごとに行うだろうという運用上の想定 がひとつです。そして、日次で判断する場合はEAの取引数の違いが原因で相関係数が過剰に小さく見積もられることがある ことも理由です。日次では相関係数がほぼゼロでも週次では高くなることもあり得ます 。その意味でも運用上の判断に用いる期間で計算した相関係数を使うことは大切です 。
また、相関係数を求める際は期間を揃える必要があります。相関係数には「時間」の要素は存在しないので、分析者自身が期間を揃えないと正しく相関係数を計算できません。(相関係数自体は2000年~2002年の結果と2004~2006年の結果の組に対しても求められます)この分析では都度分析に応じた期間を抽出したり、必要ならば改めて条件を揃えたバックテストを行って相関係数を計算します。
相関係数ですが、一般には絶対値が0.4を越えてくると相関があるとみなされることが多いので、このあたりを目安としておけば良い です。0.4を超えなければ大丈夫、ではなく、0.4を超えるEAは同時稼働しない、0.4以下でも相関係数が高いものは要注意、が推奨する考え方 です。
ただ、これはポートフォリオを目視判断と経験に基づいて選択するのではなく、平均分散アプローチに基づいて選択する際には話が変わってきます。詳しくは書きませんが、平均分散アプローチの立場ではポートフォリオの分散(標準偏差)はポートフォリオ内のEAの相関係数(正確には共分散)も用いて計算します。この場合は相関係数が小さくても影響が出る可能性がある点に注意してください。
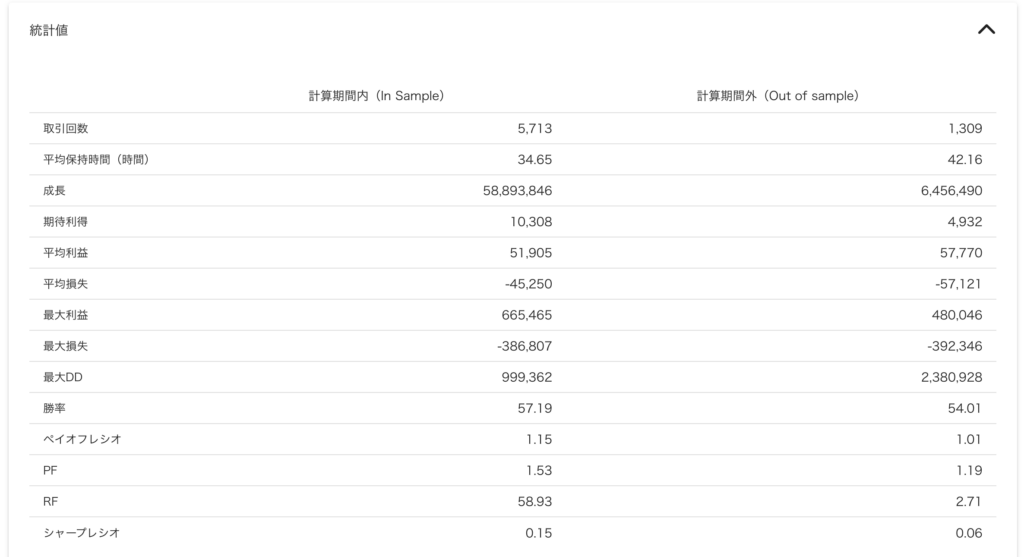
以下は、「損益特性と投資効率」「勝率と損益特性」で取り上げたEAに対して、公式のバックテストを使って相関係数を計算した例です。期間は公式バックテストの共通期間2010年01月04日~2015年12月30日を含む週としています。
まず、例として取り上げた中でスキュー・勝率-PRの切り口で似た特性を持つEAが存在しないMultiLogicShot_EA とLegato USDJPY に注目します。この2つのEAに対して相関係数が0.2を超えるEAは存在しておらず、スキュー・勝率-PRの観点同様に相関係数で見ても似たEAはほとんど存在しません。この2つのEAは他のどのEAとも異なるロジックを採用していると考えられ、今回見たどんなEAと組合せても分散効果が得られ投資効率を改善できそうです 。
一方で、スキュー・勝率-PRの切り口で良く似た相手がいるED1 やユーティリティ・プレイヤー を見てみます。ED1 はPower_Scal との相関係数が0.443 もあり、大変良く似たエクイティカーブを持っていそうです。もう少し詳しく見ると、ED1 もPower_Scal も取引通貨はEURUSDで同じ、時間足はM1とM5で異なりますが短期足という点は変わらないため、全体のエクイティカーブとしても良く似たのだと考えられます。この2つは作者が同じであるため、同一ロジックを使いまわして作成したのかもしれません。この2つを同時に動かす意味がないとは言いませんが、別の分散対象候補のEAを動かした上で証拠金的に余裕がある場合のみ同時稼働すべき です。ユーティリティ・プレイヤー についても同様で、スキュー・勝率-PRの観点で近い位置にいるCounterQとの相関係数が0.3を超えており、同時稼働には注意が必要 です。なお、この2つのEAはどちらもUSDJPY M5が投資対象です。ユーティリティ・プレイヤー は他にもRECOBA Triple Swing M5 、特にEURJPY との相関係数が0.23程度あるので同時稼働には注意が必要です。それ以外のEAは0.1前半以下の相関係数しかないので、相関係数の切り口で見れば同時稼働に大きな問題はなさそうです。スキュー・勝率-PRの切り口での類似性と合わせてポートフォリオを検討すれば、よく分散したポートフォリオを作成できます 。